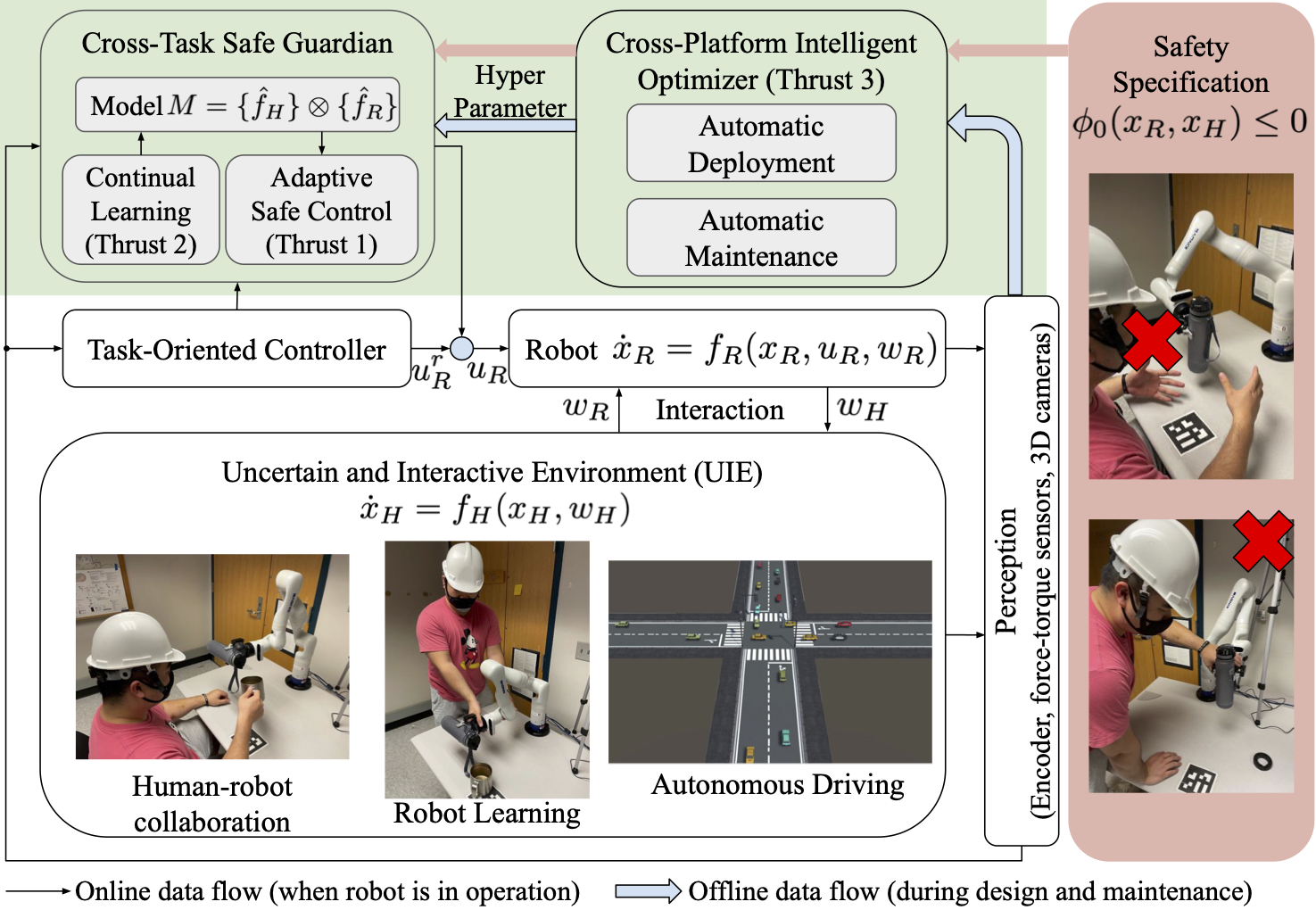
Overview

The research objective of this proposal is to study the design principles to achieve optimal lifelong safety of autonomous robotic systems in uncertain and interactive environments (UIEs). For example, this capability will enable industrial collaborative robots to safely and optimally work with unfamiliar human workers in novel tasks throughout the robots’ lifetime. UIEs are the most challenging environments for autonomous systems because they contain other intelligent entities who will react to the ego robot in unknown manners. The safety requirements are represented as constraints on the choices of the autonomous systems to achieve their tasks. Our goal is to optimally augment existing systems (existing hardware platforms with task-oriented controllers) with advanced cross-task safe guardians that will monitor and modify the nominal task-oriented actions. To avoid expensive case-by-case tuning and maintenance, we aim to automate the deployment of the safe guardians and make them self-repairable. The fundamental research question is: how to design and synthesize the safe guardians so that autonomous systems can optimally meet safety constraints throughout their lifetime in UIEs?

Problem Challenges

While existing methods are able to guarantee safety given a well-defined system dynamic model, there are several major challenges to deploy safe guardians for systems in UIEs: 1) It is difficult (if not impossible) to fully anticipate what autonomous robots may encounter in their lifetime. 2) Sometimes failures are inevitable (out of the robot’s control) and how to deal with failures still requires extensive study. 3) Existing solutions require extensive manual case-by-case modeling and tuning.

Research Goal

To address challenge I and achieve lifelong safety, we will equip the cross-task safe guardian with the following capabilities: 1) Continual learning to track the time-varying dynamics of the UIEs (thrust 2); 2) Adaptive safe control to adjust the control strategy according to newly learned dynamic models (thrust 1). To address challenges II and III and achieve optimality in lifelong safety, we will equip the safe guardians with a cross-platform intelligent optimizer that can automatically optimize the safe guardians and account for inevitable failures (thrust 3). The optimality refers to: 1) Optimal task performance when safety is assured. 2) Optimal actions before inevitable failures, i.e., minimize impact. 3) Optimal actions after any failure, i.e., never make the same mistake again. The optimizer will enable knowledge sharing for all guardians to learn from others’ successes and mistakes.

Thrust 1. Safe Control Synthesis

Safe control is synthesized in two steps.

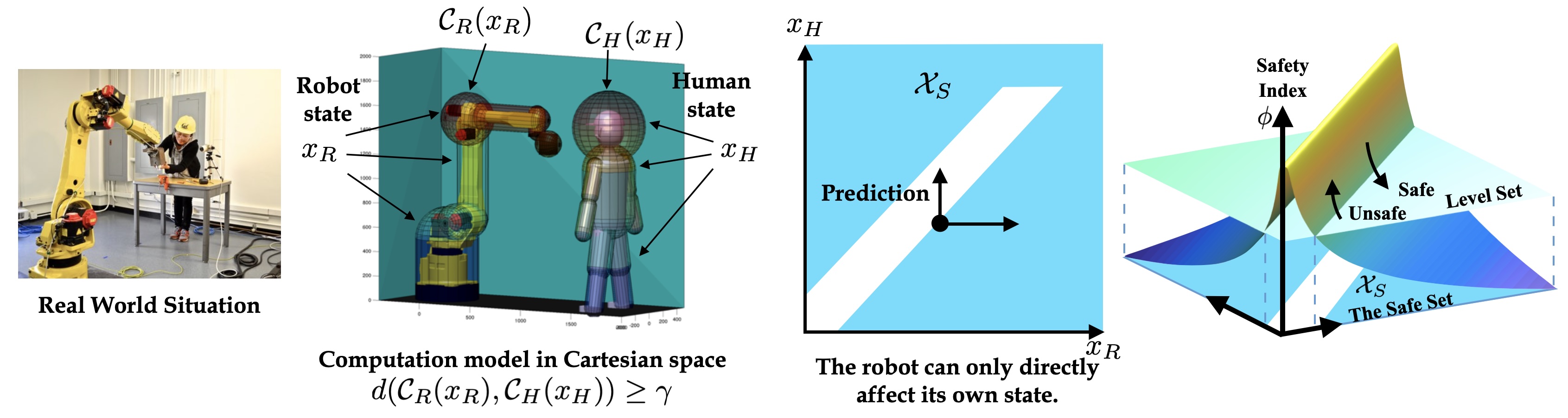
The first step is similar to “planning,” where we synthesize an energy function $\phi:x\mapsto \mathbb{R}$ given the safety specification $\phi_0$ and the system model $\dot x = f(x,u)$ for $f\in M$, such that:
- The low-energy states are safe, i.e., $\Phi_{\leq 0}:=\lbrace x\mid \phi(x)\leq 0\rbrace \subseteq \lbrace x\mid \phi_0(x) \leq 0\rbrace$.
- There always exists a feasible control input to dissipate the energy, i.e., $U_S(x)$ defined as $\lbrace u_R\in\Omega\mid \dot\phi(x)\leq -\eta(\phi),\forall f\in M\rbrace$ is always $\emptyset$, where $\dot\phi(x)=\nabla_{x}\phi \cdot f$. The set $U_S(x)$ is called the set of safe control, and $\Phi_{\leq 0}$ is called the forward invariant set. The scalar function $\eta:\mathbb{R}\mapsto \mathbb{R}$ is a design parameter, which should be non-decreasing and $\eta(0)\geq 0$.
The second step is to generate the real-time control signal, where we map the reference control $u^r$ to $U_S(x)$:

\[u = \arg\min_{u\in U_S({x})} \|u - u^r\|.\]

1.1 Safety Index Synthesis

We provided an efficient way to parameterize $\phi$ in (Liu & Tomizuka, 2014), setting $\phi_{\alpha} = \max \lbrace \hat{\phi}_{\alpha},\phi_0 \rbrace$ with $\hat{\phi}_{\alpha} = c+\phi_0^* + k_1\dot \phi_0 + k_2\ddot{\phi}_0 +\ldots + k_n \dot{\phi}_0^{(n)}$, where:

$c \geq 0$,
$\phi_0^*(x)\leq 0 \Longleftrightarrow \phi_0(x)\leq 0$,
and the roots of $1+k_1s+k_2s^2+\cdots k_ns^n=0$ are negative real.

We proved that $\phi_\alpha$ satisfies the two requirements if $\alpha = [c,\phi_0^*,n,k_1,\ldots,k_n]$ are properly chosen. Intuitively, the higher-order terms are introduced to ensure that the safety index has a relative degree of one to the robot control, and the term $\phi_0^*$ is introduced to nonlinearly shape the gradient of $\phi$. And both ${\phi}_\alpha$ and $\hat{\phi}_\alpha$ are called safety indices.

For a typical second-order system, e.g., systems that are controlled through torque or acceleration, we can define $\hat{\phi}_\alpha = c+d_{min}^n-d^n +k\dot d$ where $d$ is the smallest relative distance from the ego agent to the obstacle; and $d_{min}$ is the minimum distance requirement. Then the safety index synthesis problem is essentially figureing out the correct parameters $c,n,k$ such that $U_S(x)$ is non-empty, i.e., there alwasy exist a feasible safe control.

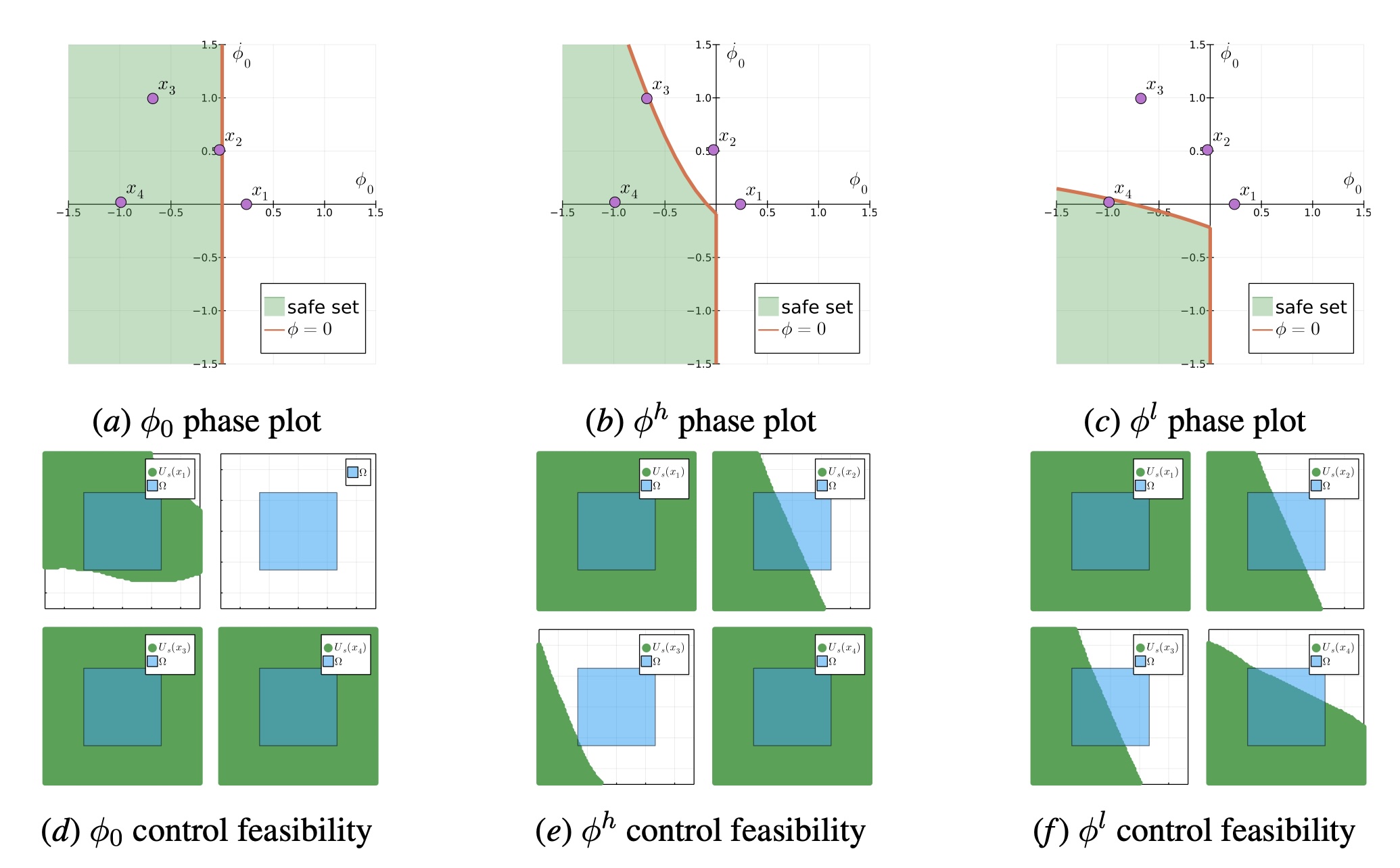
In our prior work (Wei & Liu, 2022), we use evolutionary optimization to find the parameters $\alpha$. The figure below shows the phase plots and control feasibility plots for three cases, the original safety specification, the hand-tuned safety index, the CMA-ES optimized safety index. The first row shows the phase plot for different safety index. And the second row shows the control spaces at four sampled states x1 to x4. The blue squares denotes the control limit Ω. The green areas are the feasible controls that satisfy the safety constraint. Before the safety index synthesis, there is no feasible control for x2. And for the manually designed safety index φh, there is almost no feasible control for x3. But for the learned safety index, the feasibility is guaranteed for arbitrary states.

CMA-ES

In (Ma et al., 2022), we studied joint synthesis of the safety index and the control policy using reinforcement learning.

1.1.1 Synthesis with adversarial optimization

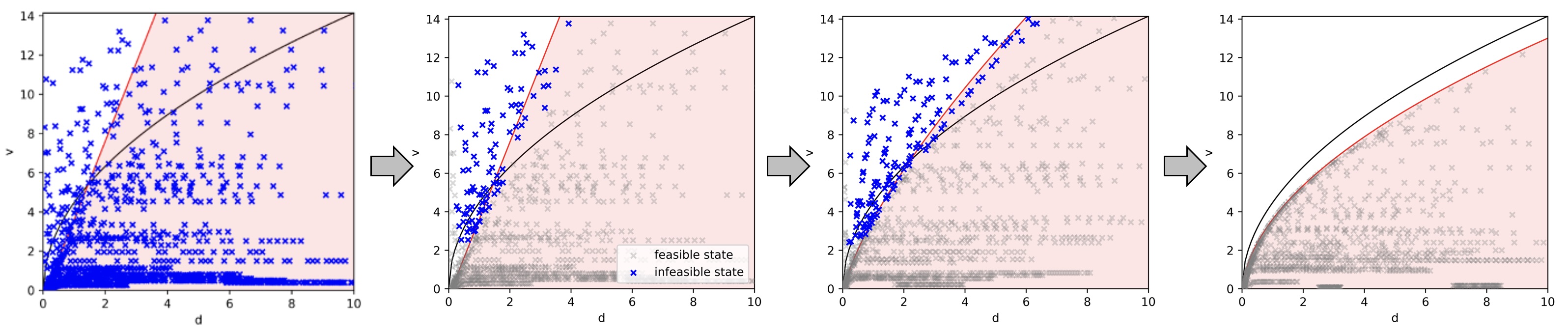
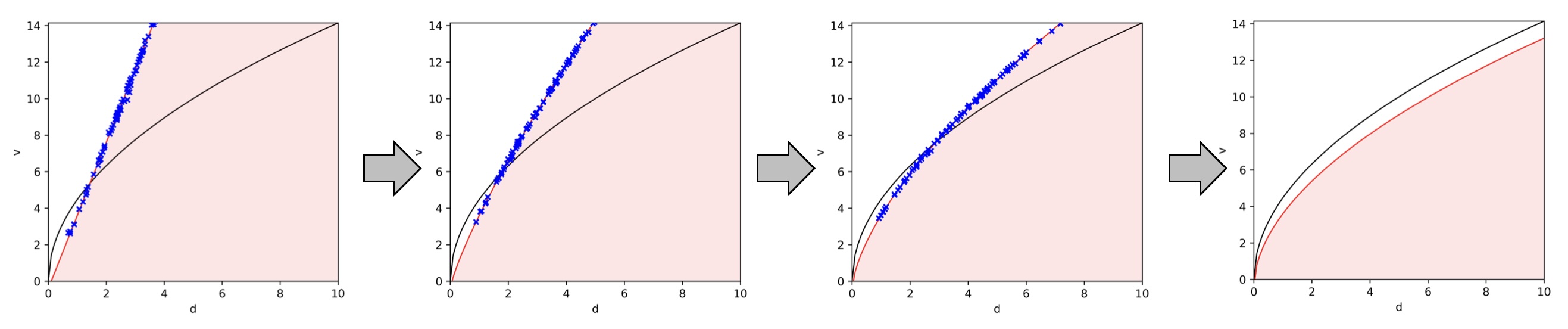
In this NSF project, we explored using adversarial optimization to optimize a neural safety index where $c$ is now a neural network and $n=1$. The method consists of a learner-critic architecture, in which the critic gives counterexamples of input saturation and the learner optimizes a neural safety index to eliminate those counterexamples. We provide empirical results on a 10D state, 4D input quadcopter-pendulum system. Our learned safety index avoids input saturation and maintains safety over nearly 100% of trials.

[C53] Safe Control Under Input Limits with Neural Control Barrier Functions
Simin Liu, Changliu Liu and John Dolan
Conference on Robot Learning, 2022
Citation Formats:
```
    
```

1.1.2 Synthesis with sum of square programming

Our study shows that ensuring the non-emptiness of safe control on the safe set boundary is equivalent to a local manifold positiveness problem, and this problem is equivalent to sum-of-squares programming via the Positivstellensatz of algebraic geometry. In this way, we can avoid sampling during the safety index synthesis, and provide stronger formal guarantees. We developed a series of methods that leverages sum-of-squares programming to find the hyperparameters of the safety index regarding both offline synthesis and online adaptation.

[C56] Safety index synthesis via sum-of-squares programming
Weiye Zhao, Tairan He, Tianhao Wei, Simin Liu and Changliu Liu
American Control Conference, 2023
Citation Formats:
```
    
```

[C67] Safety Index Synthesis with State-dependent Control Space
Rui Chen, Weiye Zhao and Changliu Liu
American Control Conference, 2024
Citation Formats:
```
    
```

[C70] Real-time Safety Index Adaptation for Parameter-varying Systems via Determinant Gradient Ascend
Rui Chen, Weiye Zhao, Ruixuan Liu, Weiyang Zhang and Changliu Liu
American control Conference, 2024
Citation Formats:
```
    
```

[C74] Synthesis and verification of robust-adaptive safe controllers
Simin Liu, Kai S Yun, John M Dolan and Changliu Liu
European Control Conference, 2024
Citation Formats:
```
    
```

1.1.3 Black-box synthesis

For systems which are hard to explicitly model, based on our prior work on implicit safe set algorithm (Zhao et al., 2021), we developed a comprehensive sampling and synthesis strategy to achieve probabilisitic safety guarantees.

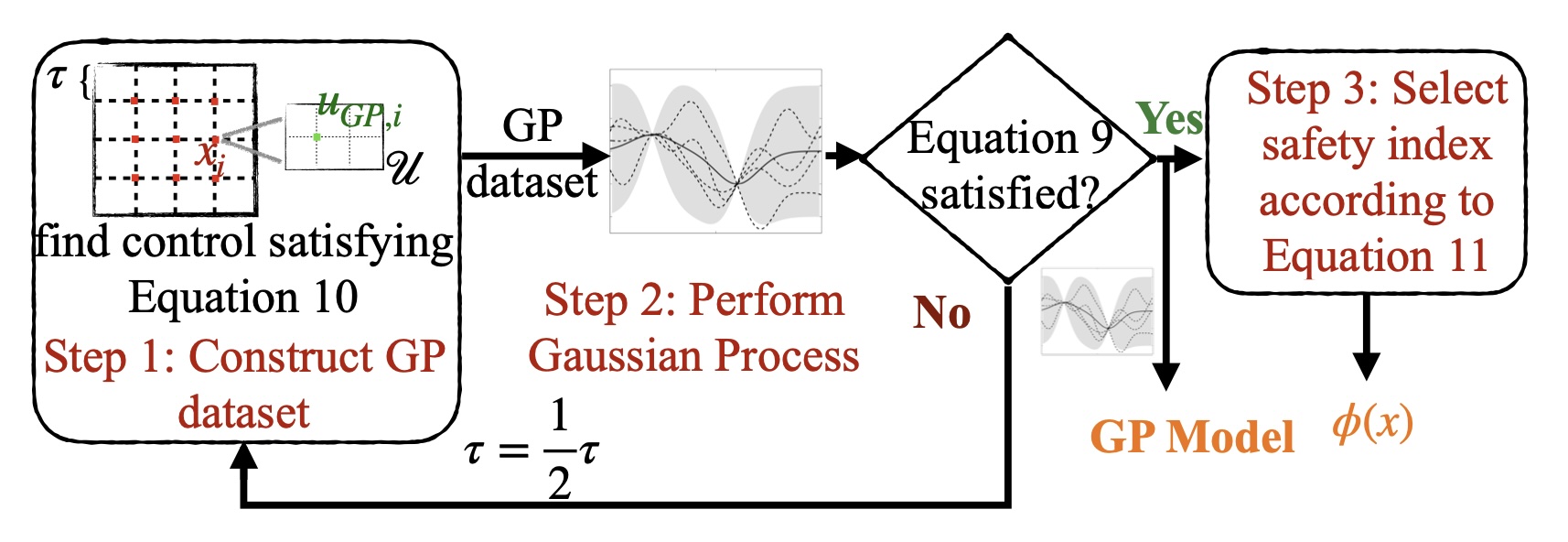
uaissa

[C57] Probabilistic safeguard for reinforcement learning using safety index guided gaussian process models
Weiye Zhao, Tairan He and Changliu Liu
Learning for Dynamics and Control Conference, 2023
Citation Formats:
```
    
```

1.1.4 Formal synthesis and verification

To address potential approximation errors inherent in safety index synthesis using data-driven approaches, we introduced the a scalable formal synthesis and verification method for neural safety functions.

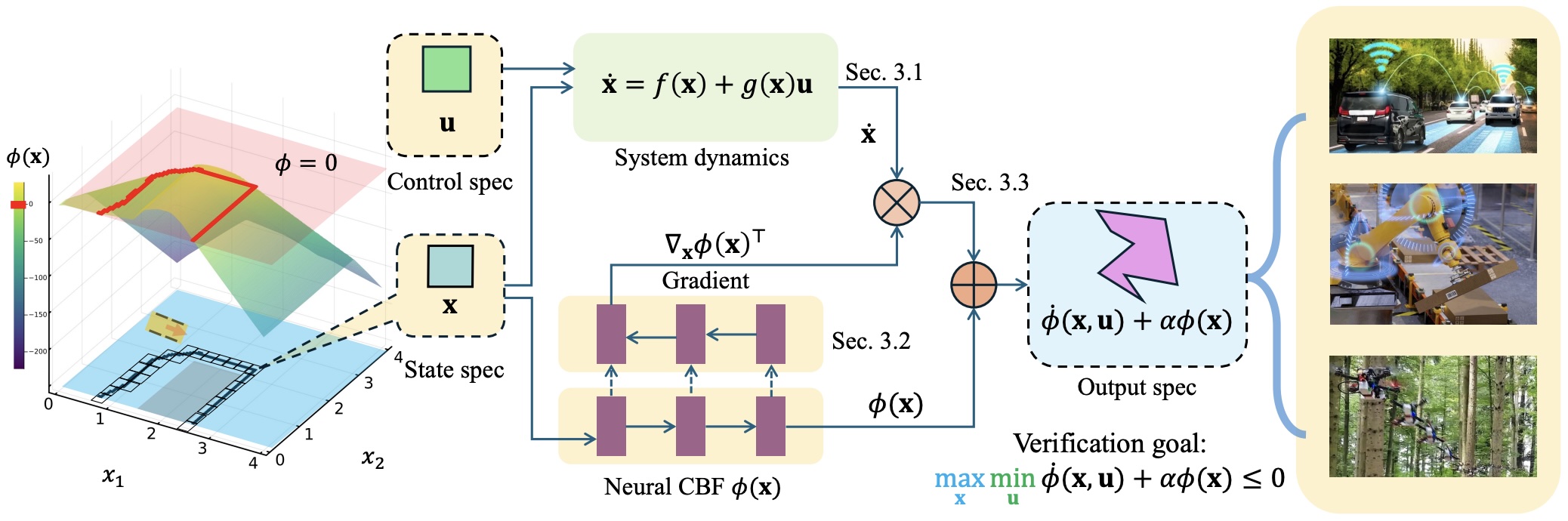
verify

[C81] Verification of Neural Control Barrier Functions with Symbolic Derivative Bounds Propagation
Hanjiang Hu, Yujie Yang, Tianhao Wei and Changliu Liu
Conference on Robot Learning, 2024
Citation Formats:
```
    
```
Abstract:

Control barrier functions (CBFs) are important in safety-critical systems and robot control applications. Neural networks have been used to parameterize and synthesize CBFs with bounded control input for complex systems. However, it is still challenging to verify pre-trained neural networks CBFs (neural CBFs) in an efficient symbolic manner. To this end, we propose a new efficient verification framework for ReLU-based neural CBFs through symbolic derivative bound propagation by combining the linearly bounded nonlinear dynamic system and the gradient bounds of neural CBFs. Specifically, with Heaviside step function form for derivatives of activation functions, we show that the symbolic bounds can be propagated through the inner product of neural CBF Jacobian and nonlinear system dynamics. Through extensive experiments on different robot dynamics, our results outperform the interval arithmetic-based baselines in verified rate and verification time along the CBF boundary, validating the effectiveness and efficiency of the proposed method with different model complexity. The code can be found at https://github.com/intelligent-control-lab/verify-neural-CBF.

1.2 Robust Safe Control During Execution

This line of research answers the following question: how can we do the projection from $u^r$ to $U_S(x)$ efficiently, especially when $U_S(x)$ is nonlinear (which typically happens when there are uncertainties in models)?

1.2.1 Non-conservative robust safe control

Model mismatches prevail in real-world applications. Ensuring safety for systems with uncertain dynamic models is critical. To overcome the loose over-approximation of uncertainties in prior works, we propose a control-limits aware robust safe control framework for bounded state-dependent uncertainties, leveraging Convex Semi-Infinite Programming, which is the tightest formulation for convex bounded uncertainties and leads to the least conservative control. csip

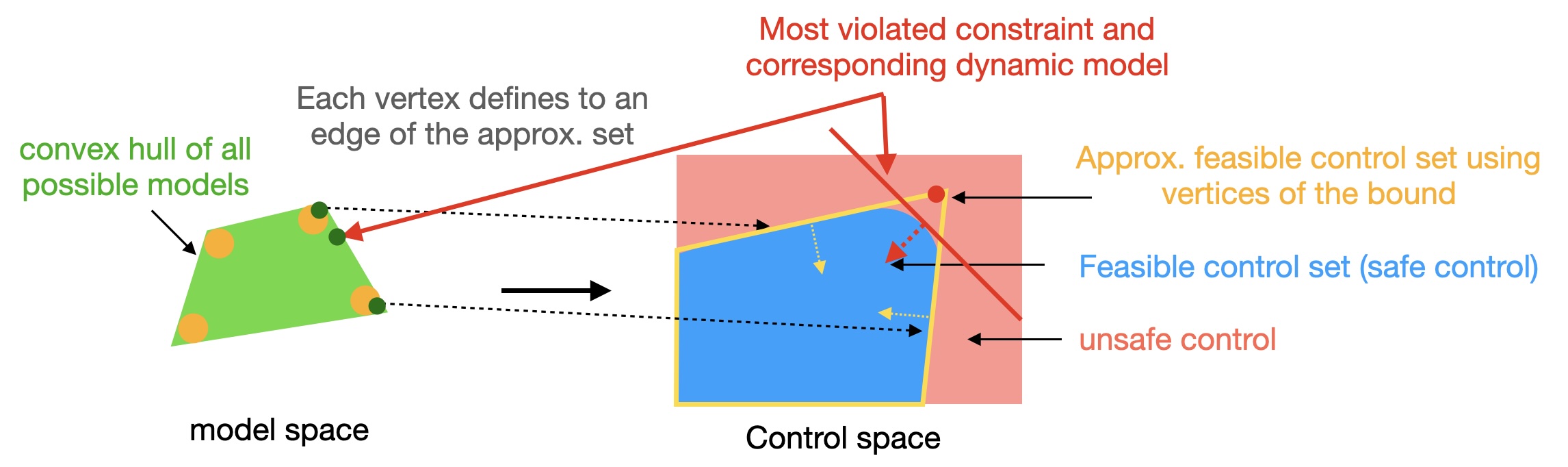
[J15] Persistently feasible robust safe control by safety index synthesis and convex semi-infinite programming
Tianhao Wei, Shucheng Kang, Weiye Zhao and Changliu Liu
IEEE Control Systems Letters, 2022
Citation Formats:
```
    
```

Existing robust safe controllers, designed primarily for uni-modal uncertainties, may be either overly conservative or unsafe when handling multi-modal uncertainties. To address the problem, we introduce a novel framework for robust safe control, tailored to accommodate multi-modal Gaussian dynamics uncertainties and control limits.

csip

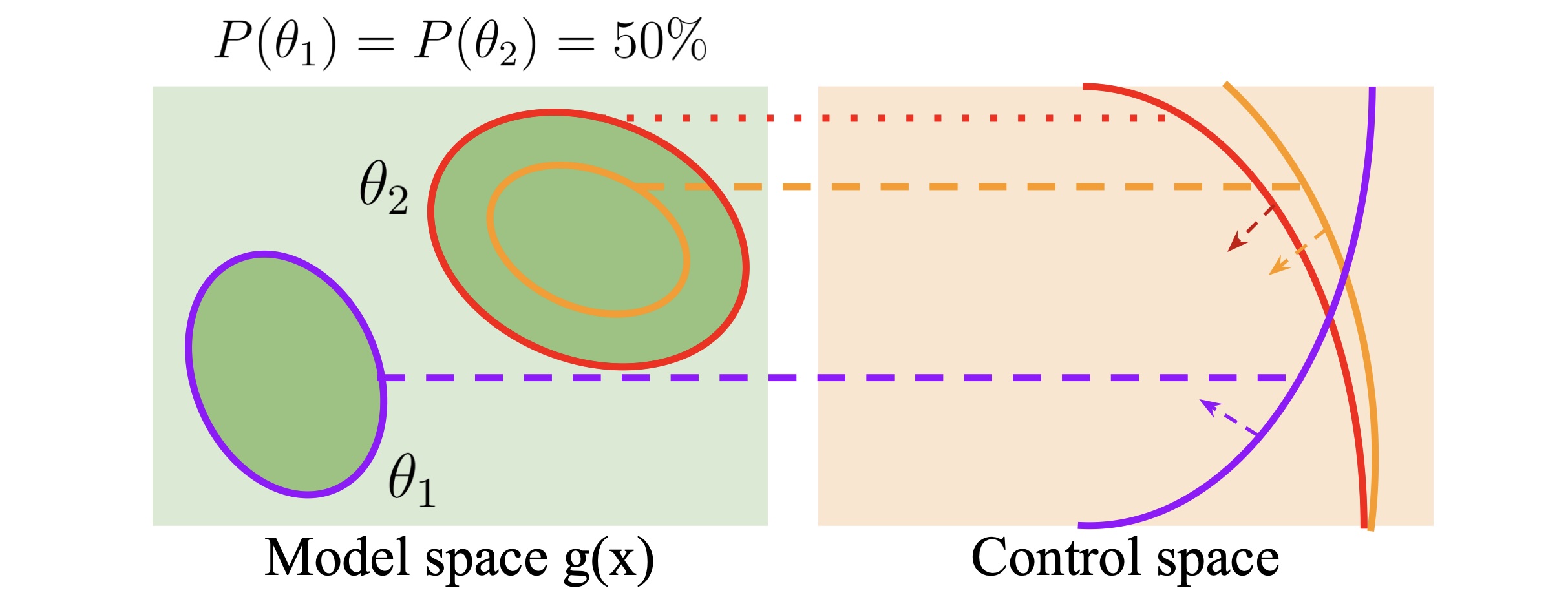
[C66] Multimodal Safe Control for Human-Robot Interaction
Ravi Pandya, Tianhao Wei and Changliu Liu
American Control Conference, 2024
Citation Formats:
```
    
```

[U] Robust Safe Control with Multi-Modal Uncertainty
Tianhao Wei, Liqian Ma, Ravi Pandya and Changliu Liu
arXiv:2309.16830, 2023
Citation Formats:
```
    
```

1.2.3 Zero-shot transfer

Considering the fact that there are redundant dynamics in high dimensional systems with respect to the safety specifications, to improve efficiency of control synthesis, we developed a novel approach called abstract safe control. The system abstraction method enables the design of safety index on a low-dimensional model. The resulting safe controller can be directly transferred to other systems with the same abstraction, e.g., when a robot arm holds different tools.

Transfer

[C63] Zero-shot Transferable and Persistently Feasible Safe Control for High Dimensional Systems by Consistent Abstraction
Tianhao Wei, Shucheng Kang, Ruixuan Liu and Changliu Liu
IEEE Conference on Decision and Control, 2023
Citation Formats:
```
    
```

1.2.4 Computationally efficient safe control over NNDM

Safe control of neural network dynamic models (NNDMs) is important to robotics and many applications. However, it remains challenging to compute an optimal safe control in real time for NNDM. To enable real-time computation, we developed methods to use sound approximations of the NNDM for real-time control.

bond

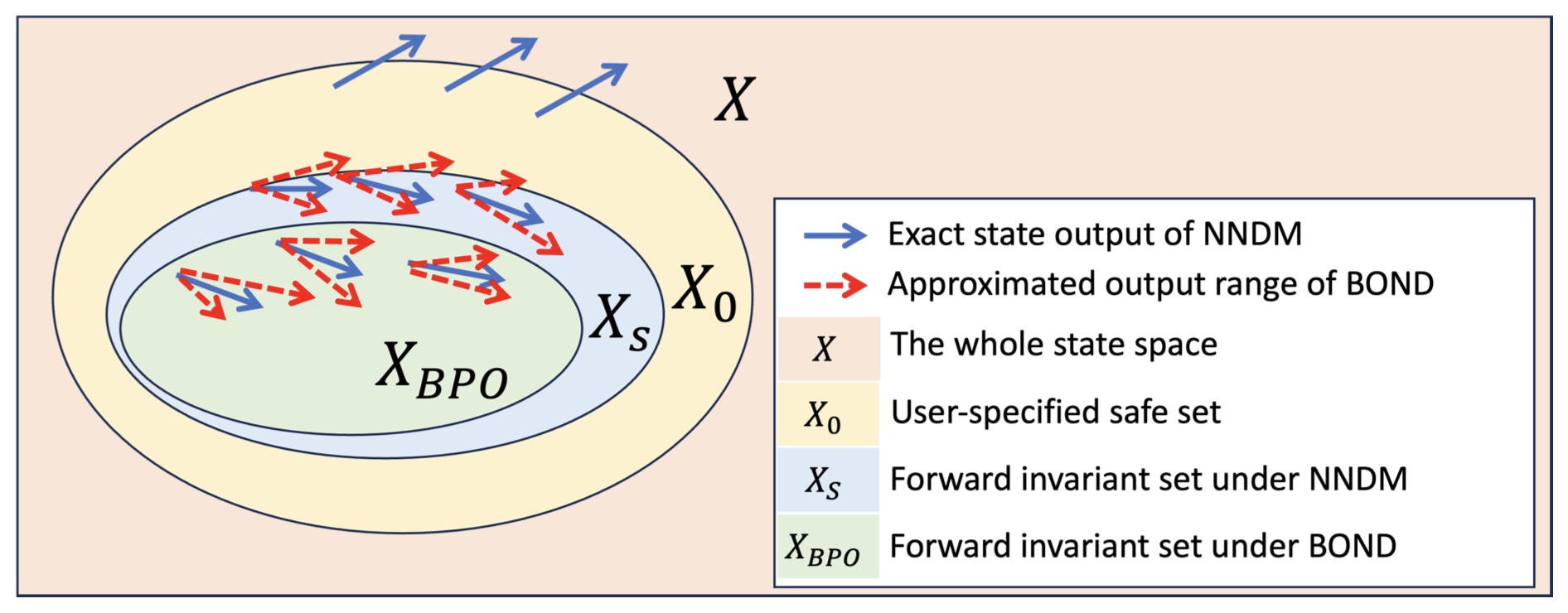
[C75] Real-Time Safe Control of Neural Network Dynamic Models with Sound Approximation
Hanjiang Hu, Jianglin Lan and Changliu Liu
Learning for Dynamics and Control Conference, 2024
Citation Formats:
```
    
```

Thrust 2. Continual Adaptation

This thrust aims to investigate data-efficient methods to continually update the model $M$ to improve closed-loop safety under time-varying dynamics (e.g., minimizing uncertainty in $M$ and enlarging the forward invariant set $\Phi_{\leq 0}$). For a model $\hat f$ parameterized by $\theta$, the continual learning at time $t$ solves the following optimization:

\[{\theta}_t = \arg\min_{\theta} \int_{\tau = 0}^{t} w_{t,\tau}\ l(\dot x^{\tau}-\hat f^{\theta}(x^{\tau},\ldots)) d\tau.\]

The parameter estimate $\theta_t$ minimizes the weighted sum of previous fitting errors (with data $x^\tau$ and loss $l$ for all $\tau$). Our prior works (Cheng et al., 2019) (Abuduweili et al., 2019) (Abuduweili & Liu, 2021) let the weights decay exponentially under the assumption that more recent data is more relevant, i.e., $w_{t,\tau} := \lambda^{t-\tau}$ where $\lambda \in [0,1]$ is the forgetting factor. The optimization is solved recursively using error feedback:

\[\dot\theta_t = \beta_t \cdot \text{feedback}(\nabla_{\theta_{t}}\hat f^{\theta_{t}}, \dot x^{t} - \hat f^{\theta_{t}}(x^{t},\ldots)),\]

where $\beta_t$ is the learning rate at time $t$, and the feedback term depends on the gradient of the model and the prediction error. Using this approach on deep neural network-based human models (missing reference) and vehicle models (Si et al., 2019), we empirically showed that time-varying dynamics can be tracked and the ground truth trajectories lie in the set of possible trajectories predicted by $M$ with almost probability one (since unexpected rare events happen in reality). To improve sample efficiency (i.e., tracking with faster convergence and smaller uncertainty), we designed a curriculum learning method (Abuduweili & Liu, 2020) to distinguish hard samples (i.e., error belonging to a certain empirical range) from simple samples and then increase the weights for hard samples. This approach significantly increases the model accuracy (i.e., tracking correctly with smaller uncertainty).

However, the remaining challenges are that existing methods that learn parametric models with scarce data are not always optimal for closed-loop safe control. There is room to further reduce the approximation error.

We aim to investigate safety-driven data-efficient continual learning from two aspects: what to learn from (data) and how to learn (algorithm). In terms of what to learn from, we let the system not only passively receive data but also actively gather information to minimize uncertainty regarding the safety constraint in the future. As for how to learn, we study algorithms to maximize information extraction from existing data, especially those are more safety-critical.

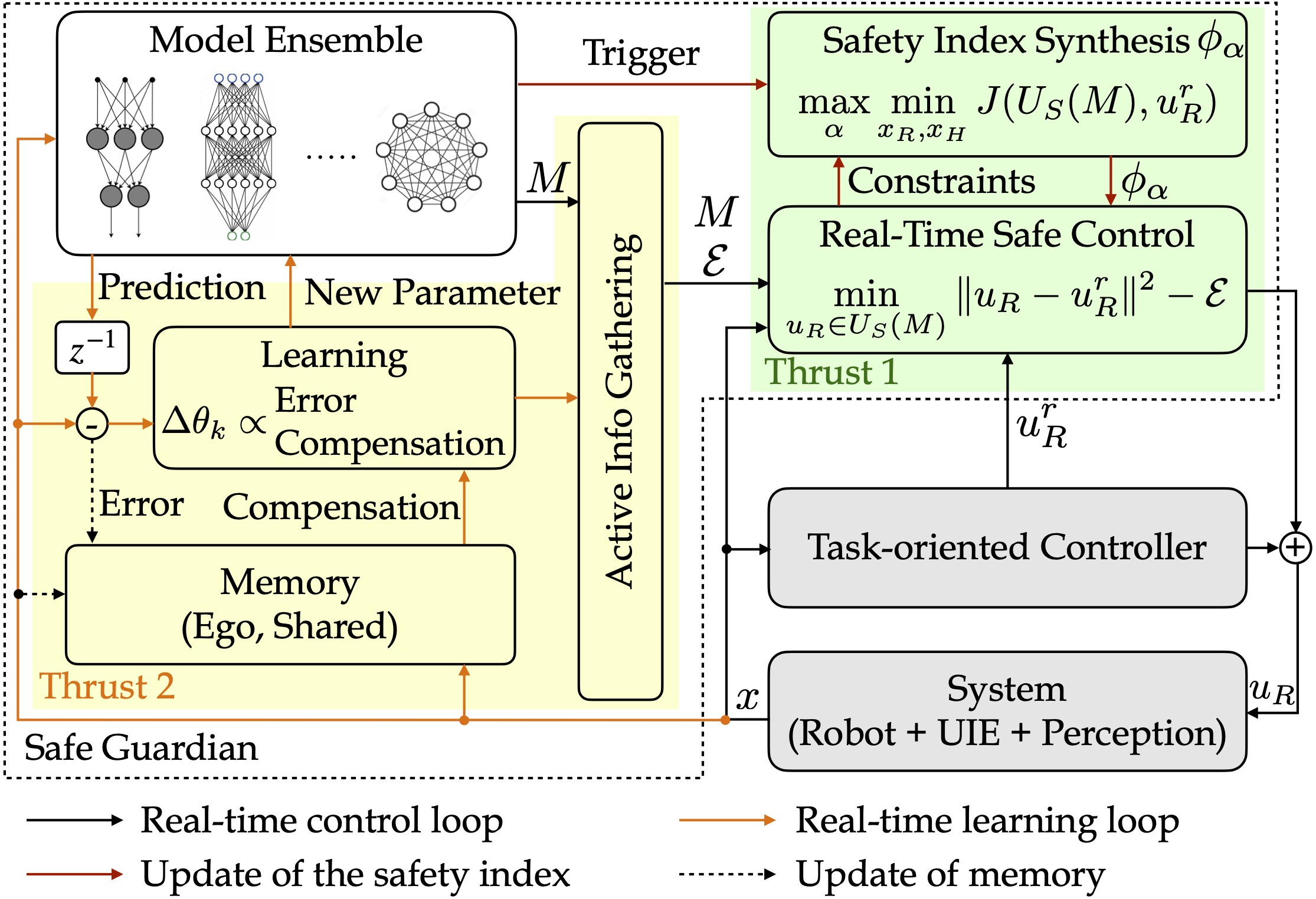
diagram

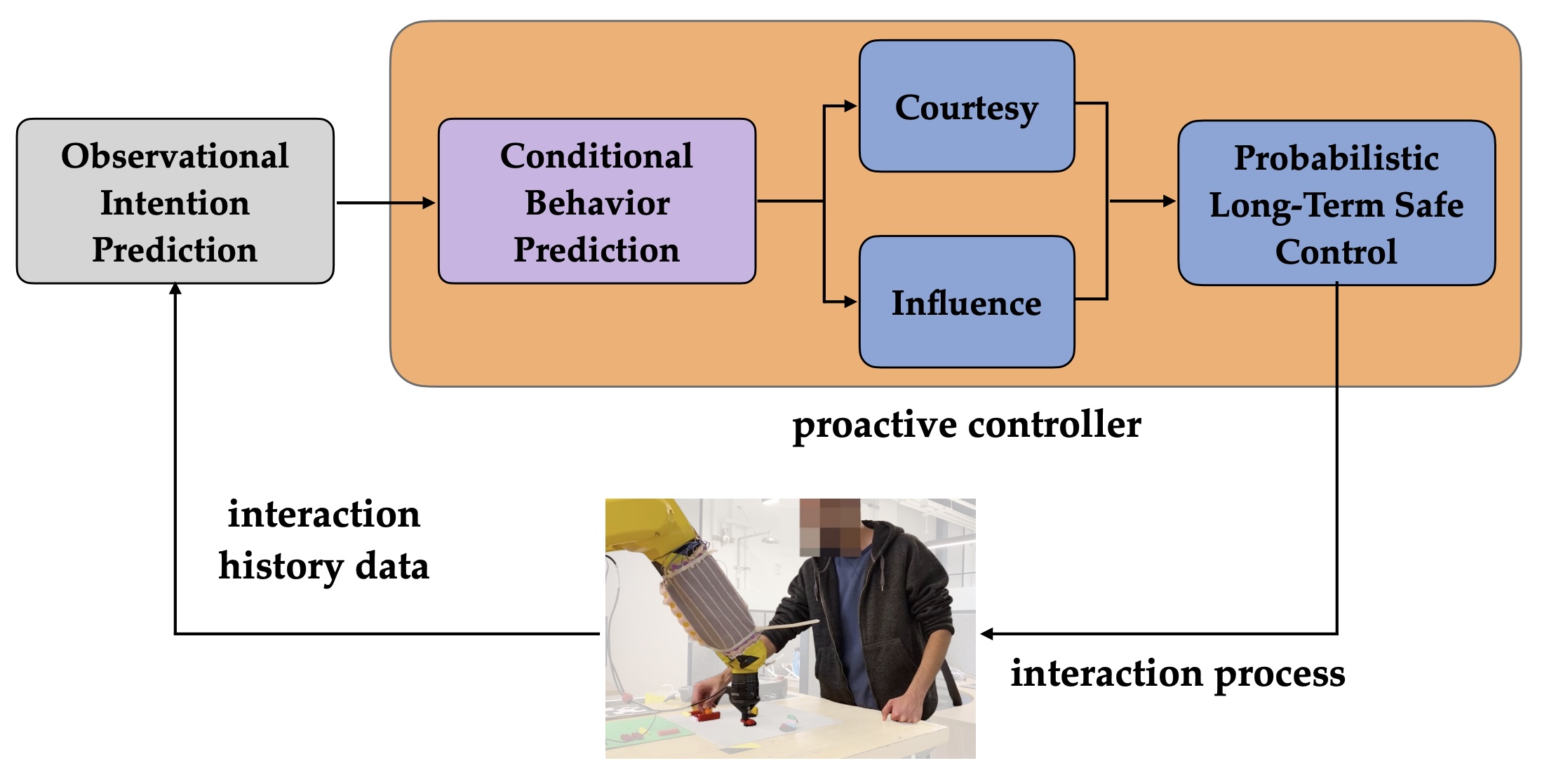
2.1 Safety-Driven Dual Control

Our research in this area aims to balance courtesy and influence in safe control during human-robot interactions and to develop explanations that enhance collaboration efficiency. These works represent significant advancements in proactive and efficient collaboration strategies between humans and robots, particularly in multi-agent settings.

courtesy

[C46] Safe and Efficient Exploration of Human Models During Human-Robot Interaction
Ravi Pandya and Changliu Liu
IEEE/RSJ International Conference on Intelligent Robots and Systems, 2022
Citation Formats:
```
    
```
Abstract:

Many collaborative human-robot tasks require the robot to stay safe and work efficiently around humans. Since the robot can only stay safe with respect to its own model of the human, we want the robot to learn a good model of the human in order to act both safely and efficiently. This paper studies methods that enable a robot to safely explore the space of a human-robot system to improve the robot’s model of the human, which will consequently allow the robot to access a larger state space and better work with the human. In particular, we introduce active exploration under the framework of energy-function based safe control, investigate the effect of different active exploration strategies, and finally analyze the effect of safe active exploration on both analytical and neural network human models.

Video:

[C72] Towards Proactive Safe Human-Robot Collaborations via Data-Efficient Conditional Behavior Prediction
Ravi Pandya, Zhuoyuan Wang, Yorie Nakahira and Changliu Liu
IEEE International Conference on Robotics and Automation, 2024
Citation Formats:
```
    
```
Video:

[C73] Multi-Agent Strategy Explanations for Human-Robot Collaboration
Ravi Pandya, Michelle Zhao, Changliu Liu, Reid Simmons and Henny Admoni
IEEE International Conference on Robotics and Automation, 2024
Citation Formats:
```
    
```
Video:

2.2 Continual Model Learning

Recognizing the difficulty of learning from scarce and heterogeneous data, we innovatively designed several recalling strategies to enahance model learning.

courtesy

[C65] Online Model Adaptation with Feedforward Compensation
Abulikemu Abuduweili and Changliu Liu
Conference on Robot Learning, 2023
Citation Formats:
```
    
```
Video:

[J20] Bioslam: A bioinspired lifelong memory system for general place recognition
Peng Yin, Abulikemu Abuduweili, Shiqi Zhao, Lingyun Xu, Changliu Liu and Sebastian Scherer
IEEE Transactions on Robotics, 2023
Citation Formats:
```
    
```
Video:

Thrust 3. Automatic Deployment

This thrust aims to develop a systematic, automatic, and resource-aware approach to deploy and maintain the safe guardian in various applications. The resource limits include constraints on memory capacity, computation capacity, and communication bandwidth. The deployment requires optimizing the hyperparameters of the system for some performance criterion under resource limits. The maintenance requires handling of the failure cases that are not fully covered during deployment.

3.1 Meta-Control: LLM-Enabled Control Synthesis

We investigated methods to automate the deployment of robot controllers across diverse scenarios by leveraging large language models (LLMs). This effort culminated in the development of Meta-Control, the first LLM-enabled automatic control synthesis approach. Meta-Control leverages LLMs to mimic human reasoning processes, utilizing extensive control knowledge in a structured, systematic manner. This innovative approach, guided by Socratic principles of inquiry, enhances efficiency and scalability in control system design.

[C83] Meta-Control: Automatic Model-based Control Synthesis for Heterogeneous Robot Skills
Tianhao Wei, Liqian Ma, Rui Chen, Weiye Zhao and Changliu Liu
Conference on Robot Learning, 2024
Citation Formats:
```
    
```
Abstract:

The requirements for real-world manipulation tasks are diverse and often conflicting; some tasks require precise motion while others require force compliance; some tasks require avoidance of certain regions while others require convergence to certain states. Satisfying these varied requirements with a fixed state-action representation and control strategy is challenging, impeding the development of a universal robotic foundation model. In this work, we propose Meta-Control, the first LLM-enabled automatic control synthesis approach that creates customized state representations and control strategies tailored to specific tasks. Our core insight is that a meta-control system can be built to automate the thought process that human experts use to design control systems. Specifically, human experts heavily use a model-based, hierarchical (from abstract to concrete) thought model, then compose various dynamic models and controllers together to form a control system. Meta-Control mimics the thought model and harnesses LLM’s extensive control knowledge with Socrates’ "art of midwifery" to automate the thought process. Meta-Control stands out for its fully model-based nature, allowing rigorous analysis, generalizability, robustness, efficient parameter tuning, and reliable real-time execution.

Video:

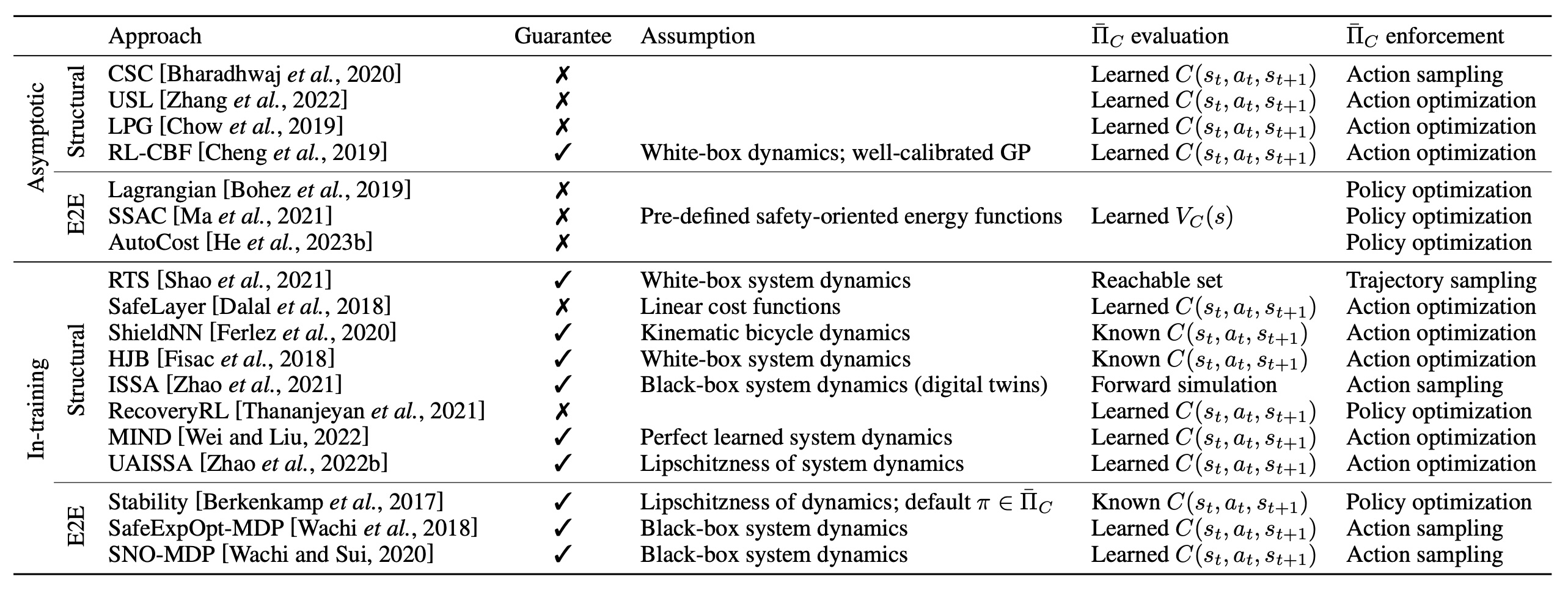
3.2 Safe Policy Learning

This line of work investigated methods for direct safe policy learning.

survey

[C60] State-wise safe reinforcement learning: A survey
Weiye Zhao, Tairan He, Rui Chen, Tianhao Wei and Changliu Liu
International Joint Conferences on Artificial Intelligence, 2023
Citation Formats:
```
    
```

[C77] Absolute Policy Optimization: Enhancing Lower Probability Bound of Performance with High Confidence
Weiye Zhao, Feihan Li, Yifan Sun, Rui Chen, Tianhao Wei and Changliu Liu
International Conference on Machine Learning, 2024
Citation Formats:
```
    
```

Real World Applications

application

Applications in Robot Arms

[J16] A hierarchical long short term safety framework for efficient robot manipulation under uncertainty
Suqin He, Weiye Zhao, Chuxiong Hu, Yu Zhu and Changliu Liu
Robotics and Computer-Integrated Manufacturing, 2023
Citation Formats:
```
    
```

Applications in Legged Robots

[C78] Agile But Safe: Learning Collision-Free High-Speed Legged Locomotion
Tairan He, Chong Zhang, Wenli Xiao, Guanqi He, Changliu Liu and Guanya Shi
Robotics: Science and Systems, 2024
Outstanding Student Paper Award Finalist
Citation Formats:
```
    
```

Testbed Development and Education

GUARD: Safety Benchmark

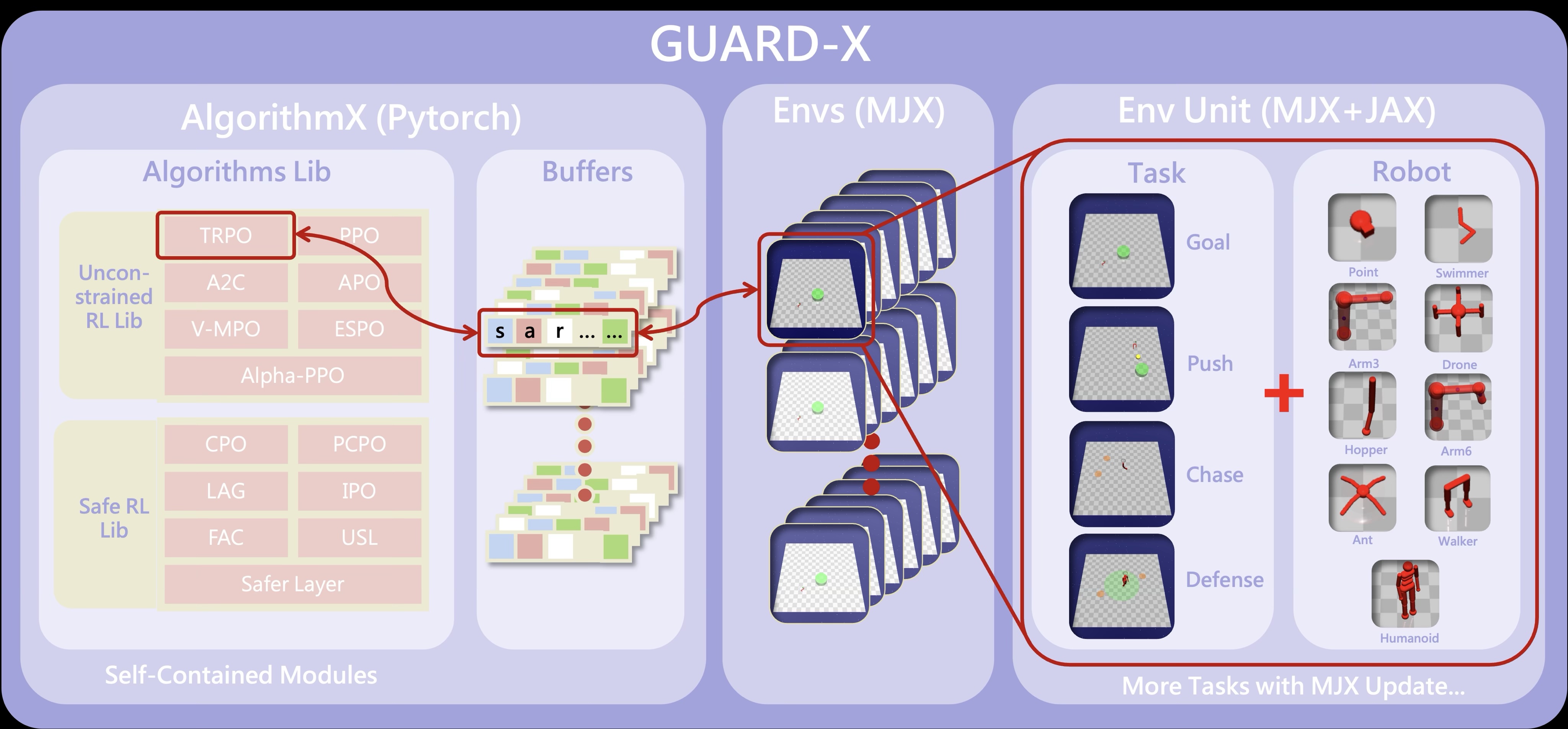
application

We developed a safety benchmark, GUARD, using the state-of-the-art Mujoco simulator. The benchmark consists of a variety of robots, tasks, safety requirements, and pre-implemented algorithms.

GUARD Repository

SPARK: Safe Humanoid Toolbox

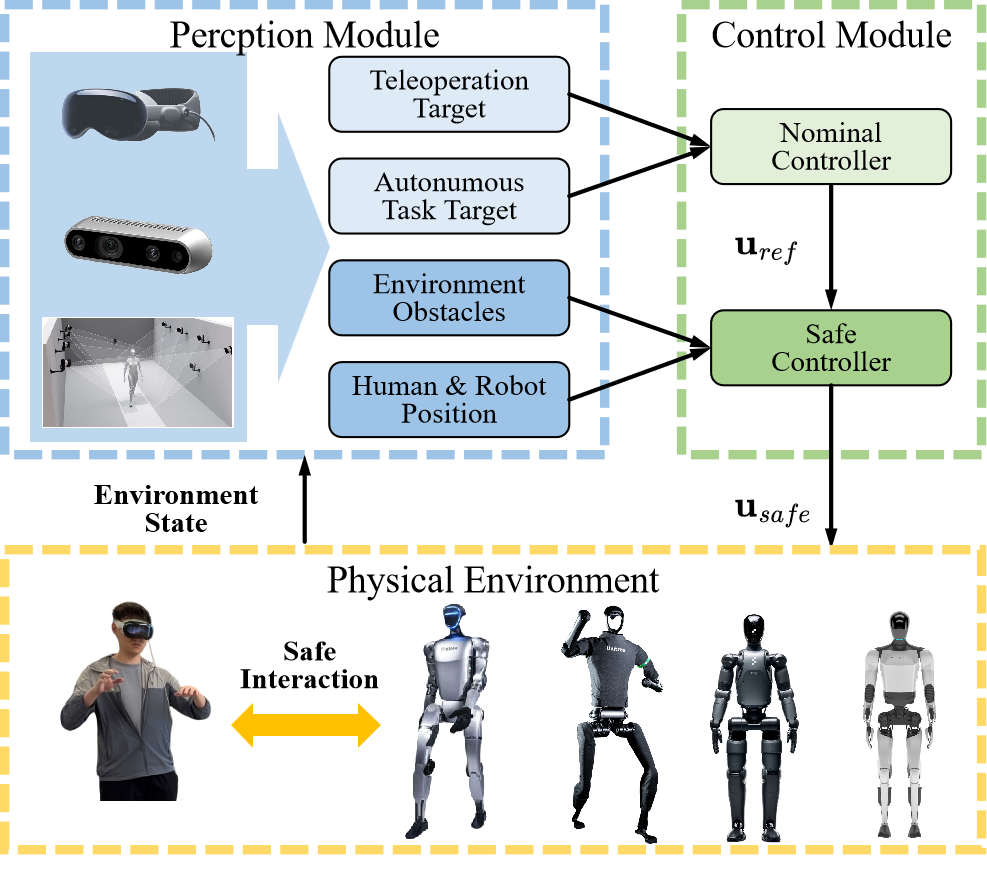
spark

We developed the Safe Protective and Assistive Robot Kit (SPARK), a modular toolbox for ensuring safety in humanoid autonomy and teleoperation. By serving as a fail-safe mechanism, SPARK significantly enhances the safety of existing humanoid systems, advancing the field of safe humanoid robotics. Spark is also integrated into my course 16-883 Provably Safe Robotics.

Associated PhD Thesis

[T2] State-wise Safe Learning and Control
Weiye Zhao
PhD Thesis, 2024
Citation Formats:
```
    
```
Abstract:

Ensuring safety by persistently satisfying hard state constraints is a critical capability in the fields of reinforcement learning (RL) and control. While RL and control have achieved impressive feats in performing challenging tasks, the lack of safety assurance remains a significant obstacle for real-world applications. Consequently, the research focus has shifted towards developing methods that meet stringent safety specifications in uncertain environments, driving the field of safe learning and control. In the realm of safe control, energy function-based methodologies allocate diminished energy levels to safe states while orchestrating secure control laws to dissipate energy. However, prevailing safe control methods necessitate explicit analytical models of the dynamic system, a constraint often unmet in real-world scenarios. Moreover, current safe control techniques typically presuppose an unbounded control space, a premise divergent from the bounded nature of actual control spaces in reality. This incongruity can lead to the possibility of an empty set of safe controls, thereby jeopardizing the assurance of state-wise safety. In the sphere of safe RL, extensive endeavors have been undertaken to address safety within the framework of Constrained Markov Decision Processes (CMDP), which is not capable of handling state-wise safety constraints. Furthermore, existing safe RL algorithms predominantly acquire policy learning through trial-and-error, a process that introduces inevitable unsafe exploration. This characteristic renders them unsuitable for training in real-world, safety-critical applications. In this thesis, we present groundbreaking advancements in RL and control, ensuring state-wise safety by effectively addressing these challenges: (i) For safe control, we design energy functions to ensure a nonempty set of safe controls under dynamics limits and different knowledge levels of system dynamics, which can achieve forward invariance and finite time convergence. (ii) In safe learning, we propose a set of novel policy search algorithms for state-wise constrained RL. Specifically, (a) State-wise Constrained Policy Optimization (SCPO) guarantees state-wise constraint satisfaction in expectation per iteration, (b) Absolute Policy Optimization (APO) guarantees monotonic improvement of worst-case performance per iteration, and (c) Absolute State-wise Constrained Policy Optimization (ASCPO) guarantees worst-case state-wise constraint satisfaction per iteration. The proposed approaches accommodates high-dimensional neural network policies. Furthermore, we combine benefits from safe control and learning to pioneer an algorithm generating state-wise safe optimal policies with zero training violations, a learning-without-mistakes paradigm. (iii) Lastly, we introduce a comprehensive and adaptable benchmark, the first of its kind, for safe RL and control. This benchmark caters to diverse agents, tasks, and safety constraints, while offering unified implementations of cutting-edge safe learning and control algorithms within a controlled environment.

[T3] Safeguarding and Empowering General Purpose Robots through Abstraction and Constraint Certification
Tianhao Wei
PhD Thesis, 2024
Citation Formats:
```
    
```
Abstract:

Robots are increasingly deployed across various domains, from industrial automation to domestic assistance. Ensuring that robots operate safely and intelligently is crucial to preventing potential risks such as injury, loss of life, and economic costs. This thesis addresses key challenges in deploying robots in complex real-world environments, including providing formal safety guarantees in uncertain conditions, scaling safety guarantees to realistic high-dimensional systems, allowing the robot to behave intelligently while remaining explainable and trustworthy, and ensuring the robustness of neural network components. This thesis introduces a suite of tools to tackle these challenges. The first tool, Meta-Control, synthesizes heterogeneous robot skills with a hiearchical control approach, which could decompose system-level safety requirements into module-level constraints. These constraints are categorized into control and neural network constraints. For control constraints, the toolset introduces Abstract Safe Control for hierarchical safety guarantees, Robust Safe Control for handling model uncertainty through a control-limits aware robust framework, Neural Network Dynamic Models (NNDM) Safe Control for integrating data-driven models with safety guarantees, and Benchmark of Interactive Safety for benchmarking and unifying different safe control algorithms. For neural network constraints, the toolset introduces ModelVerification.jl toolbox for verifying neural network safety specifications, online verification for online assurance under domain shifts and network update, and the Signal-to-Noise Ratio (SNR) loss method to enhance stability and robustness of neural networks. These tools enable the provision of formal safety guarantees with partially known or unknown dynamic models in uncertain, interactive environments, achieving state-of-the-art control safety and neural network safety. This allows robot arms to perform various tasks efficiently and safely, advancing the development of reliable and trustworthy general-purpose robots.

Other Resources

[C2] Control in a safe set: Addressing safety in human-robot interactions
Changliu Liu and Masayoshi Tomizuka
Dynamic Systems and Control Conference, 2014
Best Student Paper Finalist
Citation Formats:
```
    
```
Abstract:

Human-robot interactions (HRI) happen in a wide range of situations. Safety is one of the biggest concerns in HRI. This paper proposes a safe set method for designing the robot controller and offers theoretical guarantees of safety. The interactions are modeled in a multi-agent system framework. To deal with humans in the loop, we design a parameter adaptation algorithm (PAA) to learn the closed loop behavior of humans online. Then a safe set (a subset of the state space) is constructed and the optimal control law is mapped to the set of control which can make the safe set invariant. This algorithm is applied with different safety constraints to both mobile robots and robot arms. The simulation results confirm the effectiveness of the algorithm.
[C40] Safe Control with Neural Network Dynamic Models
Tianhao Wei and Changliu Liu
Learning for Dynamics and Control Conference, 2022
Citation Formats:
```
    
```
Abstract:

Safety is critical in autonomous robotic systems. A safe control law should ensure forward invariance of a safe set (a subset in the state space). It has been extensively studied regarding how to derive a safe control law with a control-affine analytical dynamic model. However, how to formally derive a safe control law with Neural Network Dynamic Models (NNDM) remains unclear due to the lack of computationally tractable methods to deal with these black-box functions. In fact, even finding the control that minimizes an objective for NNDM without any safety constraint is still challenging. In this work, we propose MIND-SIS (Mixed Integer for Neural network Dynamic model with Safety Index Synthesis), the first method to synthesize safe control for NNDM. The method includes two parts: 1) SIS: an algorithm for the offline synthesis of the safety index (also called as a barrier function), which uses evolutionary methods and 2) MIND: an algorithm for online computation of the optimal and safe control signal, which solves a constrained optimization using a computationally efficient encoding of neural networks. It has been theoretically proved that MIND-SIS guarantees forward invariance and finite convergence to a subset of the user-defined safe set. And it has been numerically validated that MIND-SIS achieves safe and optimal control of NNDM. The optimality gap is less than 10−8, and the safety constraint violation is 0.
[C41] Joint Synthesis of Safety Certificate and Safe Control Policy Using Constrained Reinforcement Learning
Haitong Ma, Changliu Liu, Shengbo Eben Li, Sifa Zheng and Jianyu Chen
Learning for Dynamics and Control Conference, 2022
Best Paper Finalist
Citation Formats:
```
    
```
Abstract:

Safety is the major consideration in controlling complex dynamical systems using reinforcement learning (RL), where the safety certificates can provide provable safety guarantees. A valid safety certificate is an energy function indicating that safe states are with low energy, and there exists a corresponding safe control policy that allows the energy function to always dissipate. The safety certificates and the safe control policies are closely related to each other and both challenging to synthesize. Therefore, existing learning-based studies treat either of them as prior knowledge to learn the other, limiting their applicability to general systems with unknown dynamics. This paper proposes a novel approach that simultaneously synthesizes the energy-function-based safety certificates and learns the safe control policies with constrained reinforcement learning (CRL). We do not rely on prior knowledge about either a prior control law or a perfect safety certificate. In particular, we formulate a loss function to optimize the safety certificate parameters by minimizing the occurrence of energy increases. By adding this optimization procedure as an outer loop to the Lagrangian-based CRL, we jointly update the policy and safety certificate parameters, and prove that they will converge to their respective local optima, the optimal safe policies and valid safety certificates. Finally, we evaluate our algorithms on multiple safety-critical benchmark environments. The results show that the proposed algorithm learns solidly safe policies with no constraint violation. The validity, or feasibility of synthesized safety certificates is also verified numerically.

Video:
[C38] Model-free Safe Control for Zero-Violation Reinforcement Learning
Weiye Zhao, Tairan He and Changliu Liu
Conference on Robot Learning, 2021
Citation Formats:
```
    
```
Abstract:

Maintaining safety under adaptation has long been considered to be an important capability for autonomous systems. As these systems estimate and change the ego-model of the system dynamics, questions regarding how to develop safety guarantees for such systems continue to be of interest. We propose a novel robust safe control methodology that uses set-based safety constraints to make a robotic system with dynamical uncertainties safely adapt and operate in its environment. The method consists of designing a scalar energy function (safety index) for an adaptive system with parametric uncertainty and an optimization-based approach for control synthesis. Simulation studies on a two-link manipulator are conducted and the results demonstrate the effectiveness of our proposed method in terms of generating provably safe control for adaptive systems with parametric uncertainty.
[C20] Human motion prediction using semi-adaptable neural networks
Yujiao Cheng, Weiye Zhao, Changliu Liu and Masayoshi Tomizuka
American Control Conference, 2019
Citation Formats:
```
    
```
Abstract:

Human motion prediction is an important component to facilitate human robot interaction. Robots need to accurately predict human’s future movement in order to efficiently collaborate with humans, as well as to safely plan its own motion trajectories. Many recent approaches predict human’s future movement using deep learning methods, such as recurrent neural networks. However, existing methods lack the ability to adapt to time-varying human behaviors. Moreover, many of them do not quantify uncertainties in the prediction. This paper proposes a new approach that uses an adaptable neural network for human motion prediction, in order to accommodate human’s time-varying behaviors and to provide uncertainty bounds of the predictions in real time. In particular, a neural network is trained offline to represent the human motion transition model. Recursive least square parameter adaptation algorithm (RLS-PAA) is adopted for online parameter adaptation of the neural network and for uncertainty estimation. Experiments on several human motion datasets verify that the proposed method outperforms the state-of-the-art approach with a significant improvement in terms of prediction accuracy and computation efficiency.
[W] Adaptable Human Intention and Trajectory Prediction for Human-Robot Collaboration
Abulikemu Abuduweili, Siyan Li and Changliu Liu
AAAI 2019 Fall Symposium Series, AI for HRI, 2019
Citation Formats:
```
    
```
Video:
[J7] Robust nonlinear adaptation algorithms for multitask prediction networks
Abulikemu Abuduweili and Changliu Liu
International Journal of Adaptive Control and Signal Processing, 2021
Citation Formats:
```
    
```
Abstract:

High fidelity behavior prediction of intelligent agents is critical in many applications,which is challenging due to the stochasticity, heterogeneity and time-varying natureof agent behaviors. Prediction models that work for one individual may not be appli-cable to another. Besides, the prediction model trained on the training set may notgeneralize to the testing set. These challenges motivate the adoption of online adap-tation algorithms to update prediction models in real-time to improve the predictionperformance. This paper considers online adaptable multi-task prediction for bothintention and trajectory. The goal of online adaptation is to improve the performanceof both intention and trajectory predictions with only the feedback of the observedtrajectory. We first introduce a generic tau-step adaptation algorithm of the multi-taskprediction model that updates the model parameters with the trajectory predictionerror in recent tau steps. Inspired by Extended Kalman Filter (EKF), a base adaptationalgorithm Modified EKF with forgetting factor (MEKFtau) is introduced. In order toimprove the performance of MEKFtau, generalized exponential moving average filter-ing techniques are adopted. Then this paper introduces a dynamic multi-epoch updatestrategy to effectively utilize samples received in real time. With all these exten-sions, we propose a robust online adaptation algorithm: MEKF with Moving Averageand dynamic Multi-Epoch strategy (MEKFMA−ME). We empirically study the bestset of parameters to adapt in the multi-task prediction model and demonstrate theeffectiveness of the proposed adaptation algorithms to reduce the prediction error.
[C21] Agen: Adaptable generative prediction networks for autonomous driving
Wenwen Si, Tianhao Wei and Changliu Liu
IEEE Intelligent Vehicles Symposium, 2019
Citation Formats:
```
    
```
Abstract:

In highly interactive driving scenarios, accurate prediction of other road participants is critical for safe and efficient navigation of autonomous cars. Prediction is challenging due to the difficulty in modeling various driving behavior, or learning such a model. The model should be interactive and reflect individual differences. Imitation learning methods, such as parameter sharing generative adversarial imitation learning (PS-GAIL), are able to learn interactive models. However, the learned models average out individual differences. When used to predict trajectories of individual vehicles, these models are biased. This paper introduces an adaptable generative prediction framework (AGen), which performs online adaptation of the offline learned models to recover individual differences for better prediction. In particular, we combine the recursive least square parameter adaptation algorithm (RLS-PAA) with the offline learned model from PS-GAIL. RLS-PAA has analytical solutions and is able to adapt the model for every single vehicle efficiently online. The proposed method is able to reduce the root mean squared prediction error in a 2.5s time window by 60%, compared with PS-GAIL.
[C26] Robust Online Model Adaptation by Extended Kalman Filter with Exponential Moving Average and Dynamic Multi-Epoch Strategy
Abulikemu Abuduweili and Changliu Liu
Learning for Dynamics and Control Conference, 2020
Citation Formats:
```
    
```
Abstract:

High fidelity behavior prediction of intelligent agents is critical in many applications. However, the prediction model trained on the training set may not generalize to the testing set due to domain shift and time variance. The challenge motivates the adoption of online adaptation algorithms to update prediction models in real-time to improve the prediction performance. Inspired by Extended Kalman Filter (EKF), this paper introduces a series of online adaptation methods, which are applicable to neural network-based models. A base adaptation algorithm Modified EKF with forgetting factor (MEKF_lambda) is introduced first, followed by exponential moving average filtering techniques. Then this paper introduces a dynamic multi-epoch update strategy to effectively utilize samples received in real time. With all these extensions, we propose a robust online adaptation algorithm: MEKF with Exponential Moving Average and Dynamic Multi-Epoch strategy (MEKF_EMA-DME). The proposed algorithm outperforms existing methods as demonstrated in experiments.

Video:

Sponsor: National Science Foundation

Period of Performance: 2022 ~ Now

Overview

Problem Challenges

Research Goal

Thrust 1. Safe Control Synthesis

1.1 Safety Index Synthesis

1.1.1 Synthesis with adversarial optimization

1.1.2 Synthesis with sum of square programming

1.1.3 Black-box synthesis

1.1.4 Formal synthesis and verification

1.2 Robust Safe Control During Execution

1.2.1 Non-conservative robust safe control

1.2.2 Multi-modal safe control

1.2.3 Zero-shot transfer

1.2.4 Computationally efficient safe control over NNDM

Thrust 2. Continual Adaptation

2.1 Safety-Driven Dual Control

2.2 Continual Model Learning

Thrust 3. Automatic Deployment

3.1 Meta-Control: LLM-Enabled Control Synthesis

3.2 Safe Policy Learning

Real World Applications

Applications in Robot Arms

Applications in Legged Robots

Testbed Development and Education

GUARD: Safety Benchmark

SPARK: Safe Humanoid Toolbox

Associated PhD Thesis

Other Resources